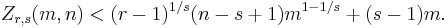Zarankiewicz problem

In the mathematical field of extremal graph theory, the Zarankiewicz problem asks how many edges can be added to a bipartite graph while avoiding a specific bipartite subgraph. Initially, the Polish mathematician Kazimierz Zarankiewicz proposed the problem of determining the maximum number of edges in an n-vertex graph with no complete bipartite graph K3,3 as a subgraph, for n ≤ 6; that is, in later notation, he asked for the values of the function Z3(n). The Kővári–Sós–Turán theorem gives a bound on the Zarankiewicz problem when the subgraph to be avoided is a complete bipartite graph.

Contents

Definition

Let Ka,b denote a complete bipartite graph with a vertices on one side of the bipartition and b vertices on the other side. Define Za,b(m,n) to be the smallest integer k such that every bipartite graph that has m vertices on one side of its bipartition, n vertices on the other side, and k edges contains a subgraph isomorphic to Ka,b.

An alternative and equivalent definition is that Za,b(m,n) is the smallest integer k such that every (0,1)-matrix of size m × n with k 1's must have a set of a rows and b columns such that the corresponding a×b submatrix is made up only of 1's.

For the specific case when m = n and a = b the shorter notation Za(n) = Za,b(m,n) may also be used.

Example

Z2(3) = 7. That is, every seven-edge subgraph of K3,3 contains a 4-cycle K2,2, but there exist 6-edge subgraphs of K3,3 with no 4-cycle. One such 6-edge graph is shown below in Figure A. However, because K3,3 only has nine edges in total, its seven-edge subgraphs are formed by removing exactly two of its edges. If the two removed edges meet at a vertex, as in Figure B, the remaining graph contains three different 4-cycles, one of which is shown in the figure. If the two removed edges do not meet, as in Figure C, the remaining graph contains two 4-cycles, one of which is shown.

The Kővári–Sós–Turán theorem

The following upper bound was established by Kővári, Sós and Turán shortly after the problem had been posed:

\displaystyle Z_{r,s}(m,n) < (r-1)^{1/s}(n-s%2B1)m^{1-1/s}%2B(s-1)m.

In fact, they proved a similar inequality for Z_{r}(n), but shortly afterwards, Hyltén-Cavallius observed that essentially the same argument can be used to prove the above inequality[1].

For constant r and s with r ≥ s, this bound is O(nm1-(1/s)+m). For r = s = 2 and m = n, this result implies that Z2(n) = O(n3/2); that is, a bipartite graph with 2n vertices and no 4-cycles has O(n3/2) edges, expressed using big O notation. This bound is within a constant factor of optimal, as the Levi graph of a finite projective plane has Θ(n3/2) edges; the absence of 4-cycles in this graph corresponds to the geometric properties that any two lines meet only in a single point and any two points are contained in only a single line of the projective plane. More generally, for r = 2, any s, and m = n, it is known that Z2,s(n,n) = Θ(n3/2) [2].

Additionally, it is known that Z3(n) = Θ(n5/3) [3]. However, except for some other specific values of r and s, it is not known whether the Kővári–Sós–Turán bound is essentially optimal. Nevertheless, some progress on this question has been made on this question in the last fifty years.

References

  1. ^ Bollobás, Béla (1978), Extremal Graph Theory, Academic Press, ISBN 0486435962 .
  2. ^ Füredi, Zoltán (1996a), "New asymptotics for bipartite Turán numbers", Journal of Combinatorial Theory, Series A 75 (1): 141–144, doi:10.1006/jcta.1996.0067 .
  3. ^ Füredi, Zoltán (1996b), "An upper bound on Zarankiewicz' problem", Combinatorics, Probability and Computing 5 (1): 29–33, doi:10.1017/S0963548300001814 .

Bibliography